villapress.blogg.se - Fraunhofer diffraction

$Fraunhofer diffraction$

$fraunhofer diffraction$

In figure, suppose BN = λ and θ = θ 1 then sin θ 1 = `lambda/"a"` BN is the path difference between secondary waves coming from A and B.

$fraunhofer diffraction$

Draw AN perpendicular to the direction of diffracted rays from point A.

This point P will be of maximum or minimum intensity because the waves reaching P will cover the unequal distance.

Consider a point P on the screen at which waves travelling in a direction making an angle θ with CP are brought to focus at P by the lens.

It is called the central or the principal maxima of the diffraction pattern.

The intensity of light is maximum at the point P o.

The optical path difference between all these wavelets is zero and hence they interfere in the same phase forming a bright image at P o.

The secondary wavelets from points equidistant from C in the upper and lower halves of the slit travel equal paths before reaching P o. The secondary wavelets traveling parallel to CP o come to a focus at P o.

$fraunhofer diffraction$

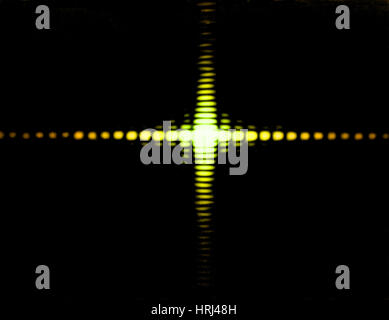
According to Huygens’ principle, each and every point of the slit acts as a source of secondary wavelets, spreading in all directions.Let D be the distance between the slit and the screen.The screen is kept in the focal plane of the lens and is perpendicular to the plane of the paper.The diffracted light is focused by a converging lens L, on a screen XY.It is illuminated by a parallel beam of monochromatic light of wavelength λ i.e., a plane wavefront is an incident on AB. The slit can be imagined to be divided into extremely thin slits or slit elements. Consider a narrow slit AB of width ‘a’, kept perpendicular to the plane of the paper.Fraunhofer diffraction due to single slit:

$Fraunhofer diffraction$